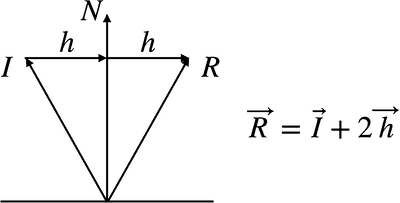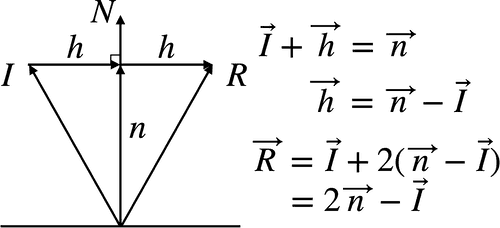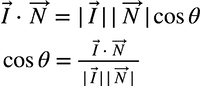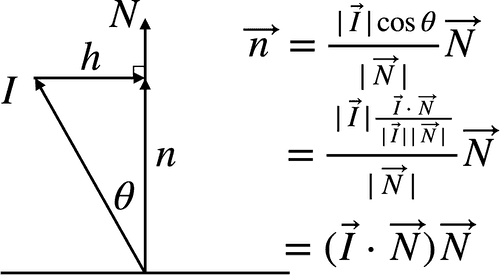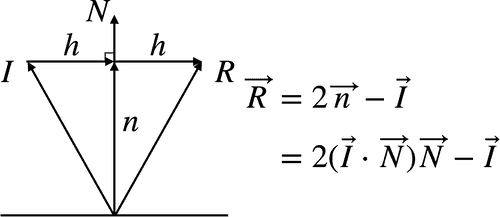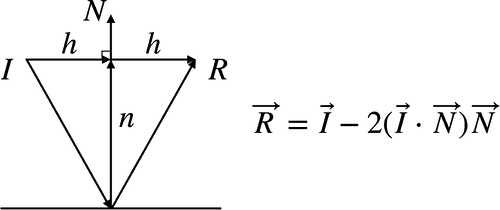こちらをみながらOpenGLでBasic Lightまでやっていて、GLSLのふとreflectについて気になったのでメモしておきます。
GLSLのreflectについて
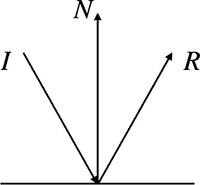
GLSLのreflect関数は、文字通り入力ベクトルに対して反射ベクトルを返す関数です。具体的には下記画像の R を返却します。
ここで、I は 反射ベクトルを求めたい入力ベクトル、N は反射面の方向を表す法線ベクトルです。 N は正規化されている必要があります。 反射ベクトルなのでIとN、RとN が成す角は等しくなります。ちなみにドキュメントに書いてあるとおり、反射ベクトルの計算方法は I - 2.0 * dot(N, I) * Nとなります。
反射ベクトルの導出
なぜ反射ベクトルが I - 2.0 * dot(N, I) * N となるのか導出してみます。
Rを下図のように求めることを考えてみます。ただし導出の兼ね合いで入力ベクトルIは、一旦反転させたものを考えます。
反射なのでIとN、RとN が成す角は等しいです。そのため上図のようにIからNに対して垂線を考えると、Iとそのベクトルhを2倍したものを足し合わせるとちょうどRになります。
また、下図のようにIからNの垂線の足が成すベクトルnを考えます。nを用いると、Rは 2n - Iと書き直せます。
nはIをNに射影したベクトルで、一般に射影ベクトルと呼びます。nは、Nと同じ方向を向いているため、nとNの長さがわかれば求まります。 さらに三角関数から、下図のようにnの長さはIの長さを用いて表現できます。
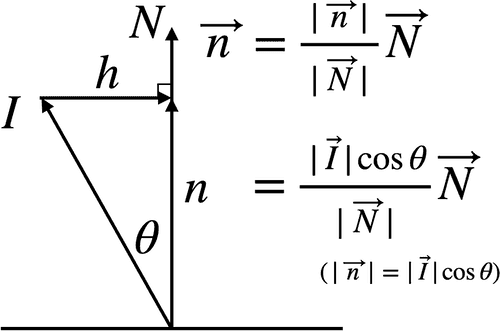
θはIとNが成す角で、cosθは内積を用いて下記のように計算できます。
上記と、Nは正規化されているので単位ベクトルなため(つまり長さが1)、先程のベクトルnは下図のように書き表すことができます。
これでベクトルnを既知の(というか入力値)値であるIとNで表すことができたので、最後に下図のようにRを求めます。
ただし最後にIは導出の都合で反転させていたので、下図のようにもう一度反転させます。Iはそのまま符号を入れ替えます。2 * dot(I,N) * Nの方は内積の計算の片方が逆を向くので、こちらもdot(I,N)の符号が入れ替わります。 よって、RはI - 2.0 * dot(N, I) * Nであることを示すことができました。
まとめ
GLSLのreflect関数について調べ、またその導出を行いました。
